Category: Multiobjective Optimization
-
Interval Filters for Pre-Selection in Model-Assisted Constrained Pareto Optimization
Michael Emmerich, JYU, Finland, 28.1.2026 When objective and constraint evaluations are expensive (CFD/FEM, digital-twin simulations, etc.), we often rely on Gaussian process regression (Kriging) as a surrogate. A GP does not only predict a mean vector, it also delivers uncertainty. Interpreted component-wise, this uncertainty naturally forms an axis-aligned confidence box in for objectives (and similarly…
-
How to Optimally Stack Your Books and Avoid a ‘Bad Hangover’
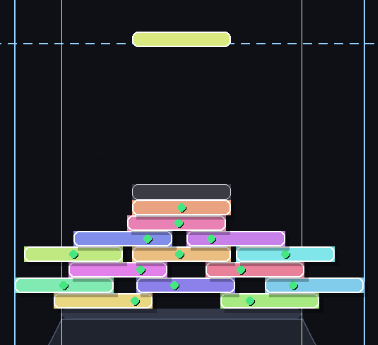
Michael T.M. Emmerich Date: 2025-12-29 Abstract It is Christmas time: books appear in cheerful piles as gifts, and in some households the morning after brings not only a “hangover” but also an ambitious attempt to stack them and exploit “overhang” beyond the edge of a table. How far can a stack of identical “books” (idealized…
-
Knee-Deep in the Mud and Climbing Out with a Clean Face
A History-Aware Multiobjective View of Escalation and De-escalation of Commitment We usually expect people to change course after negative feedback. Yet in investment and project settings the opposite is common: decision makers sometimes increase their commitment to a failing course of action. This pattern is known as escalation of commitment (Staw 1976; Staw 1981; Brockner…
-
The Hardness of Proving Hardness: Selecting Minimum Riesz Energy Subsets on a Line
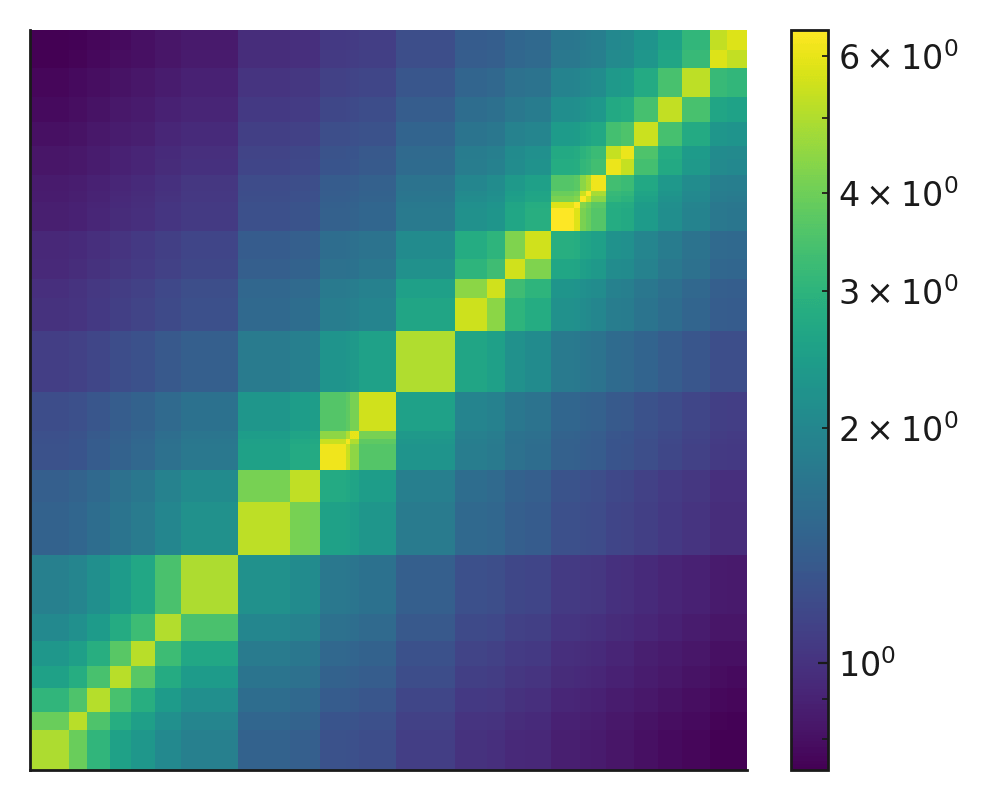
Figure: Logarithmically scaled Riesz interaction matrix for a random set of 30 points on the unit interval, with cell sizes proportional to the distances between points. Each rectangle corresponds to a pair of points: darker cells indicate stronger interactions (points that are closer on the line), while lighter cells indicate weaker interactions. Off-diagonal entries show…
-
A Tree-Free Path to Efficiently Compute the Hypervolume Indicator in Three Dimensions
In many algorithmic settings, the use of balanced trees, heaps, or other dynamic data structures is the standard way to achieve good asymptotic complexity. However, these structures can introduce memory fragmentation, unpredictable allocation patterns, garbage collection overhead, and branch-heavy execution — all undesirable in systems where performance must be deterministic and low-level behavior is important.…
-
Multiobjective Heatmaps: Landscape Visualization via ε-Dominance
Michael Emmerich, January 16th, 2025(inspired by a discussion of an application problem with Jonas Schwaab, ETH Zurich) In single-objective optimization, it is easy to visualize a function that depends on only two continuous or integer input variables by means of a heatmap plot, where the lightness indicates the achievement in the objective function, say F(x1,…
-
2-D Hypervolume Subset Selection in Python
Hypervolume Subset Selection Problem (HSSP) is a dynamic programming algorithm used to select a subset of points from a non-dominated 2D Pareto front. This subset maximizes the hypervolume (or dominated area in 2-D) covered with respect to a reference point that bounds this area from above to make it finite. Originally proposed by Auger et…
-
Uniformly Lighting the Christmas Tree: Riesz s-Energy in Action
Uniformly Lighting the Christmas Trees: Riesz -Energy in Action Michael Emmerich, December 25th, 2024 Did you ever have the problem of how to distribute candles uniformly across your Christmas Tree? Well, here is a solution from the mathematical sciences! Using the concept of Riesz -Energy, we can optimize the placement of stars or candles on…