Category: Mathematical Playground
-
How to Optimally Stack Your Books and Avoid a ‘Bad Hangover’
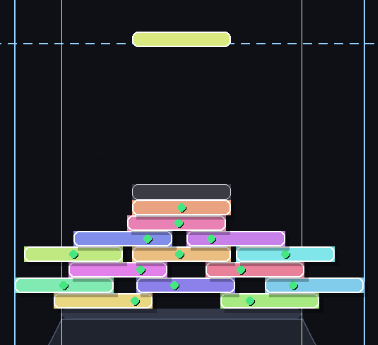
Michael T.M. Emmerich Date: 2025-12-29 Abstract It is Christmas time: books appear in cheerful piles as gifts, and in some households the morning after brings not only a “hangover” but also an ambitious attempt to stack them and exploit “overhang” beyond the edge of a table. How far can a stack of identical “books” (idealized…
-
The Hardness of Proving Hardness: Selecting Minimum Riesz Energy Subsets on a Line
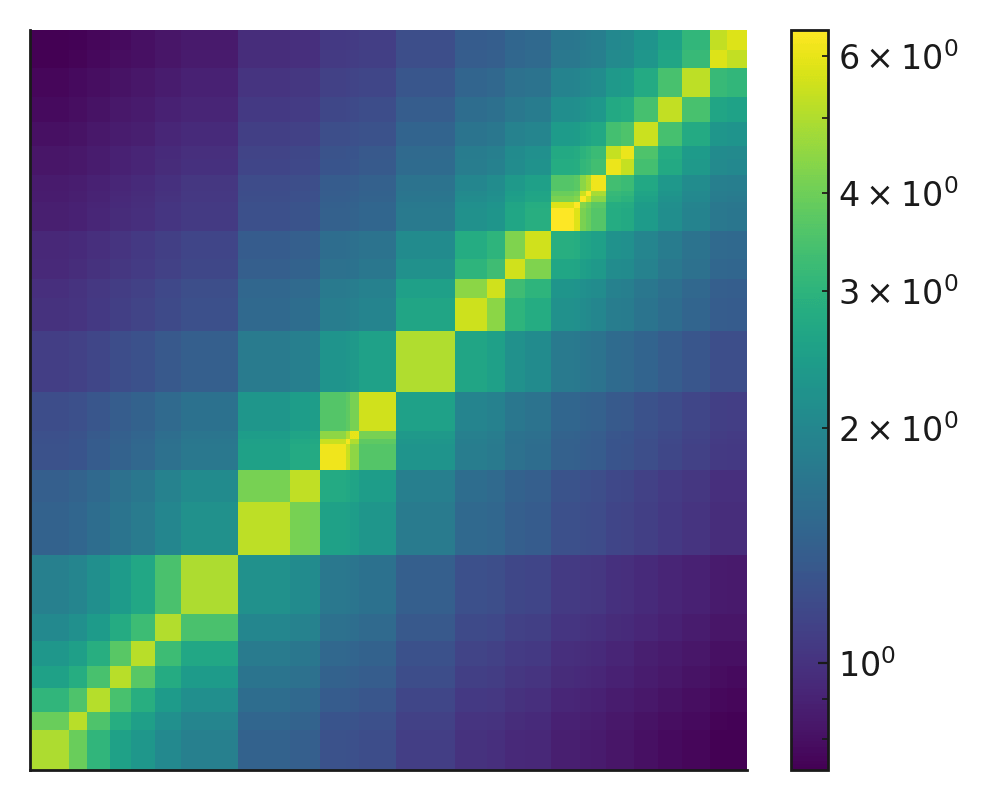
Figure: Logarithmically scaled Riesz interaction matrix for a random set of 30 points on the unit interval, with cell sizes proportional to the distances between points. Each rectangle corresponds to a pair of points: darker cells indicate stronger interactions (points that are closer on the line), while lighter cells indicate weaker interactions. Off-diagonal entries show…
-
Elegant Addition-only Prime Generation in LISP
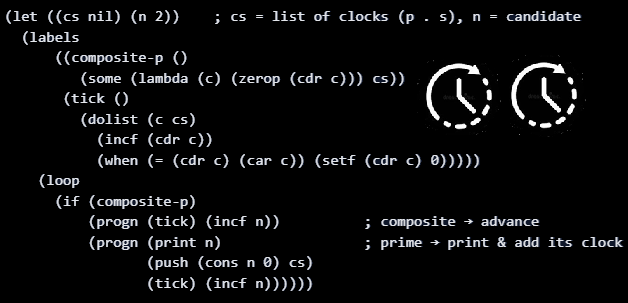
Brief history of LISP. LISP is a functional programming language that was created in the late 1950s by John McCarthy at MIT. It quickly became the lingua franca for symbolic AI because of its tiny, expressive core: homoiconic syntax (code-as-data), first-class functions/closures, macros that extend the language, and automatic memory management. McCarthy emphasized writing programs…
-
The Gumbel Distribution, Extreme Rainfall, and the Euler–Mascheroni Constant
Nature doesn’t just have averages; it has extremes—the hottest day, the strongest wind, the largest daily rainfall, the highest flood. For extremes, a universal statistical law often appears: the Gumbel distribution. In this post, we meet it through a simple and realistic story about annual maximum rainfall, learn how a basic normalization makes its shape…
-
How Computers Really Work: A countdown on a von Neumann machine

This interactive mini-simulation shows a stored-program computer in the classic von Neumann style executing a tiny machine-code program that counts down from 10 to 0. You can watch the registers and memory interact during the fetch–decode–execute cycle. It’s a compact demonstration of the model that underlies almost all modern computing—right up to the CPUs and…
-
The Tent Map – A Simple Path to Chaos
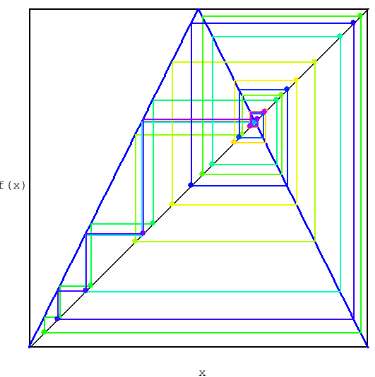
Michael Emmerich, August 20th 2025 Chaotic time series can emerge from very simple deterministic rules. The tent map is a classical example. It shows how fixed points can be unstable, how orbits diverge, and how randomness-like behavior arises from a piecewise linear rule. The Tent Map The tent map is defined on the interval by…
-
Centroid Subdivision of a Triangle: A Simple Recursion Creating a Complex Pattern
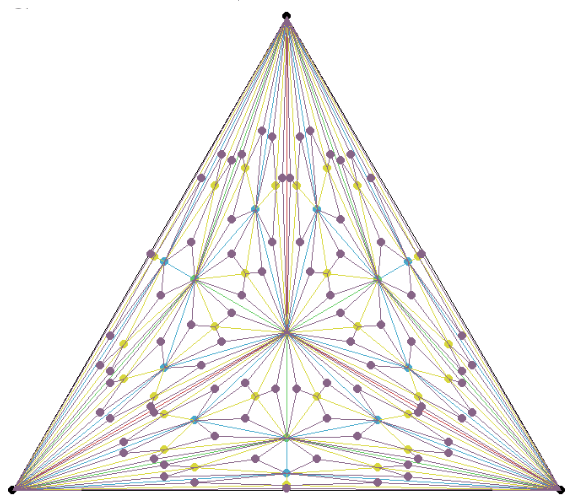
Michael Emmerich, 12 July 2025 1. Introduction A single, easily stated geometric rule—“draw the centroid of a triangle, connect it to the three vertices, and repeat recursively on the new sub-triangles”—produces a surprisingly intricate picture. This short exposition introduces the construction, shows how recursion drives the emergence of symmetry and complexity, and points out why…
-
Divisibility, Co-primes, and Euler’s Totient on the Prime Vector Grid
Michael Emmerich – 29 June 2025 1. Introduction Positive integers and their fundamental building blocks, the prime numbers, exhibit a rich combinatorial structure. This essay is part of a series that aims to derive some of the intriguing properties of integers using only elementary mathematical tools, thereby making them accessible to a broader audience. We do this…
-
Überlichtschnelle Quantenkommunikation? – Zwischen Einsteins Hypothese und Bells Experiment (in German)
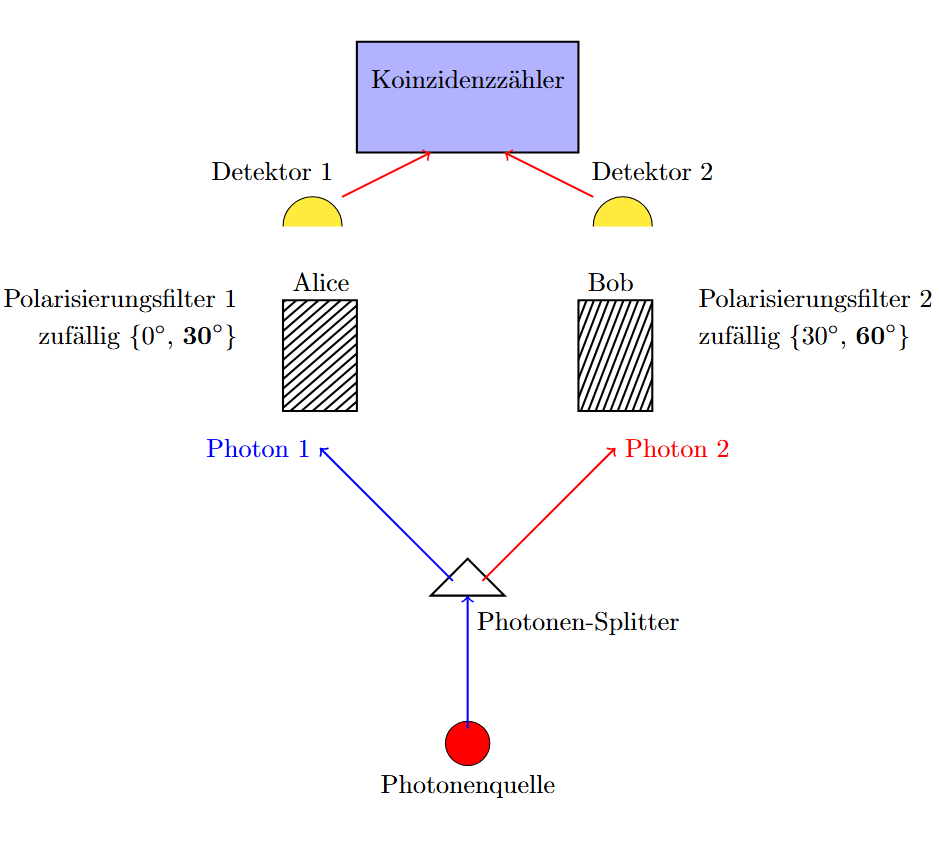
In diesem Beitrag versuche ich, auf einfache Weise darzustellen, wie mithilfe der Wahrscheinlichkeitsrechnung in einem Experiment festgestellt werden kann, ob ein System verborgene Variablen besitzt. Diese Methode ist von herausragender Bedeutung, da sie den statistischen Nachweis erbringt, dass Quantenkommunikation quasi instantan – also schneller als Lichtgeschwindigkeit – ablaufen kann. Gleichzeitig werden zentrale Prinzipien der Quantenmechanik…
-
On Prime Vectors and Unique Factorization of Rationals
Michael Emmerich, January 9, 2025 In this essay, we use the theory of prime vectors (see [1]) to provide an alternative proof of the unique factorization of integers into prime factors: Unlike earlier proofs [4], notably its first proof by Carl Friedrich Gauss [3], this extends unique factorization to rational numbers, and we also establish…