Tag: python
-
The Gumbel Distribution, Extreme Rainfall, and the Euler–Mascheroni Constant
Nature doesn’t just have averages; it has extremes—the hottest day, the strongest wind, the largest daily rainfall, the highest flood. For extremes, a universal statistical law often appears: the Gumbel distribution. In this post, we meet it through a simple and realistic story about annual maximum rainfall, learn how a basic normalization makes its shape…
-
A Tree-Free Path to Efficiently Compute the Hypervolume Indicator in Three Dimensions
In many algorithmic settings, the use of balanced trees, heaps, or other dynamic data structures is the standard way to achieve good asymptotic complexity. However, these structures can introduce memory fragmentation, unpredictable allocation patterns, garbage collection overhead, and branch-heavy execution — all undesirable in systems where performance must be deterministic and low-level behavior is important.…
-
Centroid Subdivision of a Triangle: A Simple Recursion Creating a Complex Pattern
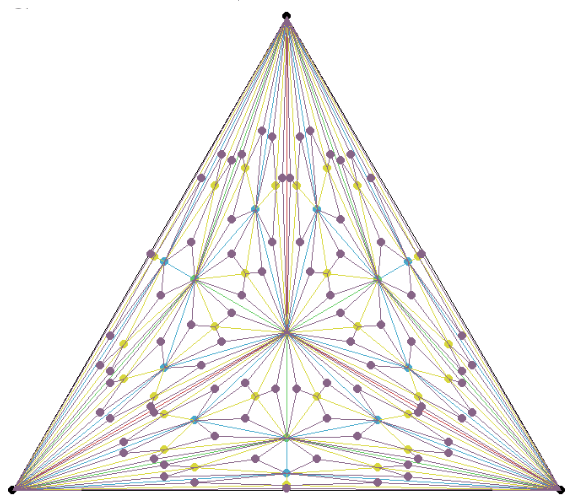
Michael Emmerich, 12 July 2025 1. Introduction A single, easily stated geometric rule—“draw the centroid of a triangle, connect it to the three vertices, and repeat recursively on the new sub-triangles”—produces a surprisingly intricate picture. This short exposition introduces the construction, shows how recursion drives the emergence of symmetry and complexity, and points out why…
-
Multiobjective Heatmaps: Landscape Visualization via ε-Dominance
Michael Emmerich, January 16th, 2025(inspired by a discussion of an application problem with Jonas Schwaab, ETH Zurich) In single-objective optimization, it is easy to visualize a function that depends on only two continuous or integer input variables by means of a heatmap plot, where the lightness indicates the achievement in the objective function, say F(x1,…
-
2-D Hypervolume Subset Selection in Python
Hypervolume Subset Selection Problem (HSSP) is a dynamic programming algorithm used to select a subset of points from a non-dominated 2D Pareto front. This subset maximizes the hypervolume (or dominated area in 2-D) covered with respect to a reference point that bounds this area from above to make it finite. Originally proposed by Auger et…
-
Uniformly Lighting the Christmas Tree: Riesz s-Energy in Action
Uniformly Lighting the Christmas Trees: Riesz -Energy in Action Michael Emmerich, December 25th, 2024 Did you ever have the problem of how to distribute candles uniformly across your Christmas Tree? Well, here is a solution from the mathematical sciences! Using the concept of Riesz -Energy, we can optimize the placement of stars or candles on…
-
Of Autumn Leaves and Coupon Collectors
Essay by Michael Emmerich, October 11th, 2024 Imagine a peaceful autumn day where leaves gently fall, covering a patch of land. The land can be represented as a grid or matrix with distinct places, each starting uncovered. As the leaves fall, they randomly land on one of these places, gradually covering the ground. But how…
-
Triangularized: Sierpinski’s Gasket and Pascal’s Triangle
Triangularized: Sierpinski’s Gasket and Pascal’s Triangle Michael Emmerich, September 28th. 2024 Introduction The Sierpinski Gasket is a fractal pattern named after the Polish mathematician Wacław Sierpiński (1882–1969). Sierpiński was a prominent figure in set theory, number theory, and topology, and he introduced several well-known fractals, including the Sierpinski Gasket (also known as the Sierpinski Triangle)…