On Prime Vectors and Unique Factorization of Rationals

Michael Emmerich, January 9, 2025

In this essay, we use the theory of prime vectors (see [1]) to provide an alternative proof of the unique factorization of integers into prime factors: Unlike earlier proofs [4], notably its first proof by Carl Friedrich Gauss [3], this extends unique factorization to rational numbers, and we also establish a one-to-one correspondence between rational numbers and prime vectors.

1. Prime Vectors

In an earlier essay [1], prime vectors were introduced to represent positive rational numbers ( ${\mathbb{Q}^+}$ ). We will provide a brief recap of the definition of prime vectors and then state the theorem and prove it. In particular, we demonstrate that rational numbers can be represented using prime vectors without assuming a priori the Fundamental Theorem of Arithmetic (FTA), and that the mapping ${P: \mathbb{Q}^+ \rightarrow \mathbb{P}_\mathbb{Q}}$ is bijective.

Definition: Prime Vectors for Integers

Let ${\{p_i\}}$ denote the sequence of prime numbers, where ${p_1 = 2, p_2 = 3, p_3 = 5, \dots}$ . Any integer ${ N > 1 }$ can be expressed as a product of primes:

$\displaystyle N = \prod_{i=1}^\infty p_i^{k_i}, \quad k_i \in \mathbb{N}_0.$

The existence of such a representation is well known and traces back to Euclid, see for instance for a proof relying only on elementary arithmetic [2].

The exponents ${k_i}$ are non-negative integers, and only finitely many are nonzero. We define the prime vector of ${N}$ as the infinite ordered list:

$\displaystyle P(N) = (k_1, k_2, \dots),$

where ${k_i}$ is the exponent of the prime ${p_i}$ in the factorization of ${N}$ . The space of prime vectors for natural numbers is denoted by ${\mathbb{P}}$ .

Definition: Prime Vectors for Rational Numbers

We extend the definition to positive rational numbers ${q \in \mathbb{Q}^+}$ . Any ${q \in \mathbb{Q}^+}$ can be uniquely expressed as:

$\displaystyle q = \prod_{i=1}^\infty p_i^{k_i}, \quad k_i \in \mathbb{Z}.$

Here, the exponents ${k_i}$ are integers (positive, negative, or zero). The prime vector of ${q}$ is the infinite ordered list:

$\displaystyle P(q) = (k_1, k_2, \dots),$

where ${k_i}$ is the exponent of the prime ${p_i}$ in the factorization of ${q}$ . The space of prime vectors for rational numbers is denoted by ${\mathbb{P}_\mathbb{Q}}$ .

Remark 1 For integers, the exponents ${k_i}$ are non-negative ( ${k_i \in \mathbb{N}_0}$ ), whereas for rational numbers, they may be any integer ( ${k_i \in \mathbb{Z}}$ ).

2. Unique Factorization

Before proving the theorem on unique factorization of rational numbers we will first proof some auxiliary lemmas.

The figure below highlights the flow of our proof.

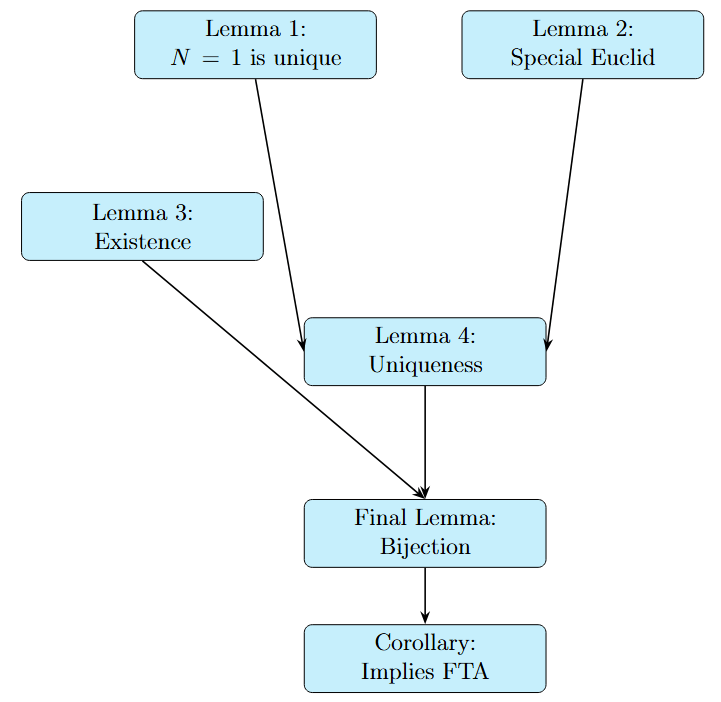
Lemma 1 (Unique Representation of ${ N = 1 }$ .) The number ${ N = 1 }$ is represented by the unique prime vector ${(0, 0, \dots)}$ , corresponding to ${ \prod_{i=1}^\infty p_i^0 = 1 }$ .

Proof: We aim to show that ${N = 1}$ can only be represented by the prime vector ${(0, 0, \dots)}$ .

1. Case: All Exponents are Zero: If ${P(1) = (0, 0, \dots)}$ , then:

$\displaystyle \prod_{i=1}^\infty p_i^{k_i} = \prod_{i=1}^\infty p_i^0 = 1,$

which satisfies the definition of ${N = 1}$ .

2. Case: One or More Exponents are Nonzero: For the product ${ \prod_{i=1}^\infty p_i^{k_i}}$ to equal ${1}$ , the contributions from the positive and negative exponents must perfectly balance:

$\displaystyle \prod_{i : k_i > 0} p_i^{k_i} = \prod_{j : k_j < 0} {p_j^{|k_j|}}.$

The left and right products can be renamed to ${A = a_1 a_2 \cdots a_n}$ , respectively ${B= b_1 b_2 \cdots b_m}$ and organized as a sorted product of primes where ${\{a_1, a_2, \dots, a_n\}}$ and ${\{b_1, b_2, \dots, b_m\}}$ are two non-overlapping multi-sets of primes. Assume, that the primes are sorted by their index in semi-increasing order: ${ a_1 \leq a_2 \leq \cdots \leq a_n \quad \text{and} \quad b_1 \leq b_2 \leq \cdots \leq b_m. }$

Assume we have chosen the naming ${a}$ and ${b}$ such that ${a_1 < b_1}$ . The strict inequality follows from the disjoint-ness of the two multi-sets. Then, since ${A = B}$ and ${a_1}$ is a factor of ${A}$ , it holds that ${a_1}$ must divide ${b_1 b_2 \cdots b_m}$ . Since ${b_1}$ is prime and ${b_1}$ is distinct to all factors ${a_i}$ , ${a_1}$ cannot divide ${b_1}$ . Therefore, ${a_1}$ must divide ${b_2 b_3 \cdots b_m}$ , due to Euclids lemma. By applying this principle iteratively, ${a_1}$ if it divides ${b_2, b_3 b_4 \cdots b_m}$ must divide ${b_2}$ or ${b_3 b_4 \cdots b_m}$ . It is impossible for ${a_1}$ to divide ${b_2}$ because the ordered list shows ${a_1 < b_2}$ and ${b_2}$ is prime. This reasoning implies ${a_1}$ must divide ${b_3 b_4 \cdots b_m}$ , reducing inductively until ${b_m}$ , leading to a contradiction. $\Box$

In the above paragraph, we used Euclid’s lemma to argue that if ${d}$ divides ${u v}$ and ${d}$ is prime, then ${d}$ must either divide ${u}$ or divide ${v}$ . However, the proof of Euclid’s lemma is quite lengthy and for this proof it suffices to proof a special case of Euclid’s lemma.

Lemma 2 (Special Case of Euclids Lemma.) Let ${d}$ denote a prime number and ${u}$ denote a number that is coprime with ${u}$ and ${d < u}$ . If ${d}$ divides the product ${u v}$ then ${d}$ must divide ${v}$ .

Proof: The lemma can be proven using only simple arithmetic by strong induction. Our proof corresponds to a proof of the auxiliary lemma in [2], case 3: We can rewrite the statement ${d}$ divides the product ${u v}$ as the statement: There exists a positive integer ${k}$ such that ${d k = u v}$ . Now, we subtract ${d v}$ from both sides, which yields ${d (k-v) = (u-d) v}$ . Since ${d}$ and ${u}$ are coprime, also ${d}$ and ${u-d}$ are coprime. Hence, by the induction hypothesis (using ${d (k-v) = (u-d) v < d k = uv}$ ), we obtain that ${u-d}$ must divide ${k-v}$ or put in other words there exists a positive integer ${k'}$ such that ${(u-d) k' = k-v}$ . Substituting ${k-v = (u-d) k'}$ into ${(u-d)k = d(k-v)}$ yields ${d (u-d) k = d (u-d) k'}$ . We divide the latter equation by ${(u-d)}$ , which is positive since ${d < u}$ , to obtain ${k=dk'}$ , which proves the result. $\Box$

Lemma 3 (Existence of Prime Factorizations of Rational Numbers) Every positive rational number ${q}$ has a prime vector representation ${(k_1, k_2, \dots )}$ , with ${q = \prod_{i=1}^\infty p_i^{k_i}, \quad p_i \in \mathbb{Z}}$ denoting primes, and ${k_i \in \mathbb{Z}}$ denoting integer exponents.

Proof: Let ${a}$ and ${b}$ denote positive integers, and ${r = a/b}$ denote the rational number we want to represent through ${a = \prod_n {p_i}^{a_i}}$ and ${b = \prod_m {p_i}^{b_i}}$ , with ${a_i \in \mathbb{N}_0}$ and ${b_i \in \mathbb{N}_0}$ . To obtain the factorization, we can use the well-known division tree algorithm [2]. Note that the positive integers are now denoted by a prime vector of ${a}$ , say ${(a_1, a_2, \dots)}$ and a prime vector of ${b}$ , say ${(b_1, b_2, \dots)}$ . Then we cancel out the terms that refer to the same prime numbers, and this yields ${\prod_m {p_i}^{a_i-b_i}}$ . $\Box$

Lemma 4 (Uniqueness of Prime Factorizations) Each positive rational number ${ N }$ has at most one prime factorization, up to the order of the factors.

Proof: Let ${ N > 1 }$ and suppose ${ N }$ has two distinct factorizations into primes: ${ N = p_1^{q_1} p_2^{q_2} \cdots p_k^{q_k} = q_1^{r_1} q_2^{r_2} \cdots q_m^{r_m}, }$ where ${p_1, p_2, \dots, p_k}$ and ${q_1, q_2, \dots, q_m}$ are primes, and ${e_i, f_j \geq 1}$ . We aim to show that ${ k = m }$ , ${ p_i = q_i }$ , and ${ e_i = f_i }$ for all ${ i }$ . Let ${ q \in \mathbb{Q} }$ denote some prime vector ${ (q_1, q_2, \dots) \in \mathbb{P}_\mathbb{Q} }$ and ${r\in \mathbb{Q}}$ has some prime vector ${ (r_1, r_2, \dots) \in \mathbb{P}_\mathbb{Q}}$ , respectively. We want to show that, if ${q = r}$ , or ${ q /r = \prod p_i^{q_i-r_i} = 1}$ then it follows that ${q_1 = r_1, q_2 = r_2, \dots}$ . Consider, this is not the case. Then at least for one entry ${ q_i \neq r_i }$ , and hence ${ (q_1 - r_1, q_2 - r_2, \dots) \neq (0, 0, \dots) }$ , which contradicts that there is only one unique representation of ${1}$ as a prime vector in ${\mathbb{P}_\mathbb{Q}}$ . $\Box$

3. Bijection between the Rationals and Prime Vectors

Based on the above unique factorization theorem of the rational numbers we prove the one-to-one correspondence of rational numbers and prime vectors as a corollary.

Lemma 5 (Bijection Between Rational Numbers and Prime Vectors) The mapping ${P: \mathbb{Q}^+ \rightarrow \mathbb{P}_\mathbb{Q}}$ , defined by associating each positive rational number ${q \in \mathbb{Q}^+}$ with its unique prime vector ${ P(q) = (k_1, k_2, \dots)}$ where ${q = \prod_{i=1}^\infty p_i^{k_i}}$ and ${k_i \in \mathbb{Z}}$ , is bijective. Specifically:

For every ${ q \in \mathbb{Q}^+ }$ , there exists a unique prime vector ${ P(q) \in \mathbb{P}_\mathbb{Q} }$ .
For every prime vector ${ (k_1, k_2, \dots) \in \mathbb{P}_\mathbb{Q} }$ , there exists a unique ${ q \in \mathbb{Q}^+ }$ .

Proof: Three statements consolidate the proof:

For every positive rational number there exists a factorization (see Lemma 3)
For every rational number the factorization is unique (see Lemma 4).
Every prime-vector represents a rational number. (This is simple; compute the product of prime numbers raised to the exponents given in the prime vector.).

$\Box$

Remark 2 This bijection implies the Fundamental Theorem of Arithmetic (FTA) for positive rational numbers. Specifically, every ${ q \in \mathbb{Q}^+ }$ can be factored as a product of primes ${ \prod_{i=1}^\infty p_i^{k_i} }$ and this factorization is unique, with exponents ${ k_i \in \mathbb{Z} }$ . This extends the classical FTA, which asserts the unique factorization of integers, to the broader domain of rational numbers. We also established the Fundamental Theorem of Arithmetic for positive integers using an alternative approach, beginning with the existence of prime vector representations of positive integers. Our proof relied only on a specific case of Euclid’s lemma. While it can be argued, that a new proof may not be strictly necessary, we believe, as noted also in [4], that presenting alternative proofs can provide valuable insights, helping mathematicians deepen their understanding of the core ideas underpinning the theorem.

Michael T.M. Emmerich, Playing with primes, emmerix.net July 29, 2024.
Michael T.M. Emmerich, Fundamental Theorem of Arithmetics: A proof from first principles, emmerix.net December 7, 2024
Gauss, C. F. (1801). Disquistiones arithmeticae. Dissertation. Königliche Gesellschaft der Wissenschaften zu Göttingen.
John W. Dawson. Why Prove it Again: Alternative Proofs in Mathematical Practice. Basel: Birkhäuser, 2015.

On Prime Vectors and Unique Factorization of Rationals

Share this:

Leave a comment Cancel reply