The Fundamental Theorem of Arithmetic: Zermelo’s proof in detail
Michael Emmerich, December 14th, 2024
Zermelo (1934) employs a proof by contradiction to establish the uniqueness of prime factorization for positive integers, demonstrating that the assumption of a non-unique prime factorization leads to a contradiction. Notably, his proof does not rely on Euclid’s Lemma. This essay reproduces Zermelo’s proof, which is somewhat tricky, with an effort to explain its steps in greater detail compared to previous works. It is important to note that the proof of the existence of prime factorization has already been covered in my previous essay, which also includes a proof of uniqueness based on Euclid’s Lemma. (Link).
Proof
- He first postulates that if there exists a positive integer with non-unique prime factorization, there must be the smallest such integer, which we call
.
- Notably, all positive integers smaller than
would have a unique prime factorization.
- Contradiction assumption: Let us show that if such a smallest number
with non-unique prime factorization exists, this leads to a contradiction:
- If
were the smallest integer with non-unique prime factorization, there would exist (at least) two distinct prime factorizations of
.
- Let us order the factors of
in the two factorizations such that
(first factorization),
(second factorization).
- Note that the two factorizations cannot have any common factor, say
for some indices
and
. If they did, we could construct a smaller integer with non-unique prime factorization than
, as dividing both factorizations by
would yield such an integer.
- Thus,
. Without loss of generality, assume
. (If
, we could simply exchange the letters
and
.)
- Define a smaller positive integer:
- The integer
is smaller than
and strictly positive because of the assumption
.
- Using basic arithmetic (the distributive law), the following equalities hold: (Eq.1):
, and (Eq.2):
.
- From the first equality,
is divisible by
.
- From the second equality,
is also divisible by
.
- Thus,
must divide either (a) one of the
, or (b)
.
- Case (a): If
divides one of the
for
, this leads to a contradiction because
(by
and the ordering
). Since
are prime, they cannot be divisible by the smaller prime
.
- Case (b): If
divides
, then
must also divide
(since
). But
is prime, and this is a contradiction because
.
- Hence, both cases (a) and (b) lead to contradictions.
- Therefore, there cannot exist a smallest integer
with non-unique factorization. q.e.d.
Zermelo, E.: Elementare Betrachtungen zur Theorie der Primzahlen. Nachr. Gesell. Wissen. Göttingen (Neue Folge) 1, 43–46 (1934)
Dawson, Jr., John W.. Why Prove it Again?: Alternative Proofs in Mathematical Practice (p. 49). Springer International Publishing. Kindle Edition.
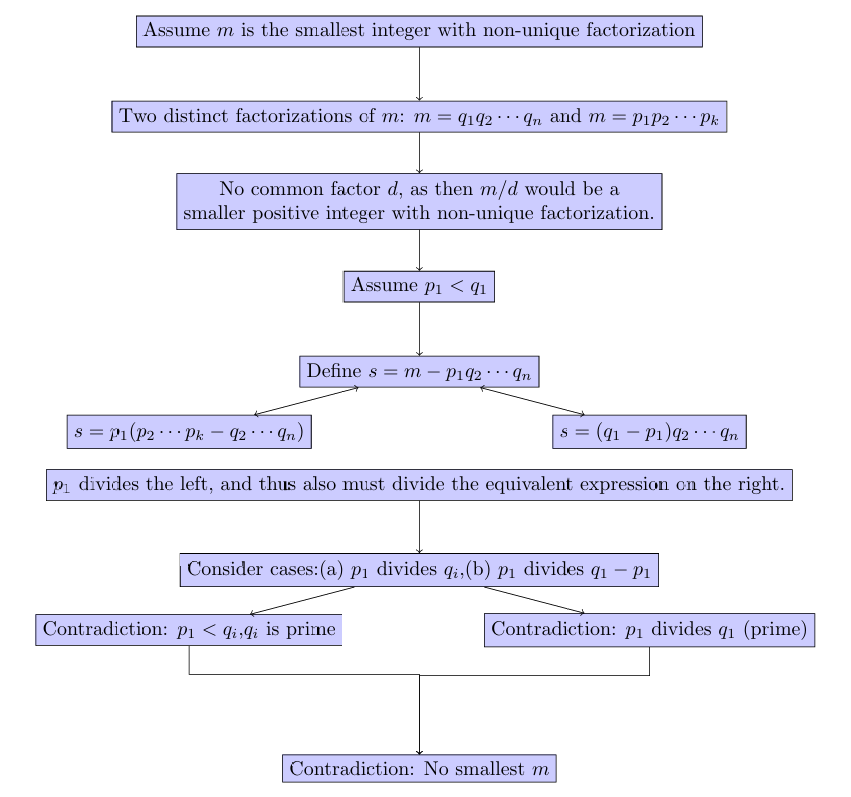
Graphical description of the structure of Zermelo’s proof.