The Partition Problem and the Possibility of an U.S. Electoral Stalemate

The Partition Problem and the Possibility of an U.S. Electoral Stalemate

Michael Emmerich, November 4th 2024

1. Integer Partitionings

This essay is about an interesting problem in computational mathematics, and its solution with integer linear programming. A didactic example is provided, that could motivate the problem and is closely related to the U.S. presidential election system, where states need to be won, each state adding a prescribed integer number to the total count of delegate votes to the result. There are 50 states and 538 electors, but typically states are won in total, and all electors of that state vote for the candidate who won the state. So can there be a stalemate?

The integer partition problem is a classic problem in combinatorial optimization and number theory. Given a set of integers, the goal is to divide them into two subsets such that the sum of elements in each subset is as equal as possible. This problem is closely related to the subset-sum problem and is a well-known NP-complete problem, meaning that no known polynomial-time algorithm can solve all instances of the problem.

2 Mathematical Formulation

Let ${ V = \{v_1, v_2, \dots, v_n\} }$ be a set of integers. The integer partition problem asks whether it is possible to partition ${ V }$ into two disjoint, i.e. non-overlapping, subsets, ${ S_1 }$ and ${ S_2 }$ , such that the sums of the subsets are equal:

$\displaystyle \sum_{v \in S_1} v = \sum_{w \in S_2} w.$

If the total sum of all integers in ${ V }$ is odd, it is immediately clear that no such partition exists. For even sums, the problem becomes challenging due to its computational complexity.

3. Time Complexity

The integer partition problem is NP-complete, which implies that, in the general case, no efficient solution exists to find an exact answer in polynomial time. Instead, solutions are often approximate or use exponential-time algorithms, such as dynamic programming or integer linear programming (ILP) formulations, which can handle small to moderately-sized instances effectively.

4. Integer Linear Programming (ILP) Formulation

The integer partition problem can be formulated as an integer linear programming (ILP) problem. By introducing binary decision variables ${ x_i \in \{0, 1\} }$ for each element ${ v_i \in V }$ , we can define a partitioning where ${ x_i = 1 }$ if ${ v_i }$ is assigned to subset ${ S_1 }$ and ${ x_i = 0 }$ if assigned to subset ${ S_2 }$ . We define a variable ${ t }$ that represents the minimum sum of either subset.

The ILP formulation becomes:

$\displaystyle \mbox{Maximize } \quad t, \mbox{ subject to} \quad \sum_{i=1}^n x_i v_i \geq t, \quad \sum_{i=1}^n (1 - x_i) v_i \geq t,$

$\displaystyle x_i \in \{0, 1\}, \quad i = 1, \dots, n$

where: ${ v_i }$ represents the electoral votes associated with each state. ${ x_i }$ is a binary variable indicating the assignment of ${ v_i }$ to either subset. ${ t }$ is the maximum possible minimum sum for both subsets.

This formulation aims to maximize ${ t }$ , ensuring that both subsets have sums that are as close as possible.

5. Application to the U.S. Electoral College

In the U.S. Electoral College, each state (and Washington, D.C.) has a fixed number of electoral votes based on population size. A presidential candidate wins the election by securing a majority of the electoral votes, with the threshold being 270 out of a total 538 votes. However, it is theoretically interesting to investigate whether the electoral votes could be divided into two groups of equal sum, resulting in a tie (269-269).

To determine if a tie is possible, we can apply the integer partition problem to the set of electoral votes. If we can partition these votes into two subsets where each subset sums to exactly 269, then a tie is possible under the current Electoral College configuration.

Using the ILP formulation above, we can test the partitioning of the electoral votes. If an equal partition exists, it indicates a potential scenario for a tied election. Otherwise, the ILP will maximize the minimum subset sum, showing the closest achievable balance.

We have written a python program and visualized the result in a pie chart (see appendix).

7. Conclusion

The integer partition problem is sometimes considered to be the easiest NP-complete problem, due the seemingly simplicity of the task to simply balance the two selections of integers. While the problem’s NP-completeness prevents efficient solutions for large instances, integer linear programming (ILP) provides a practical approach for moderate-sized sets, such as the U.S. Electoral College. By applying ILP, we can evaluate whether a tie is theoretically feasible or obtain the closest possible partition, which provides insight into the balance of electoral votes and possible tie scenarios. Formulating the ILP is also a nice, easy example of how to formulate an ILP formulation with binary variables.

The graphic illustrates the closest possible outcome in the U.S. Electoral College, with blue and red being interchangeable. In conclusion, a winner is always assured if delegates vote unanimously for their state’s winning candidate.

Remark : However, the exact law is slightly different than in this didactic essay: The U.S. Electoral College is a body established by the U.S. Constitution for electing the President and Vice President. It consists of 538 electors, with each state allocated a number of electors equal to its total number of Senators and Representatives in Congress. During a presidential election, voters in each state cast ballots to choose electors pledged to a particular candidate. These electors then meet in December to cast their votes for President and Vice President. A candidate needs a majority of 270 electoral votes to win. If no candidate reaches this majority, the election is decided by the U.S. House of Representatives.

References

Garey, M. R., and Johnson, D. S. (1979). Computers and Intractability: A Guide to the Theory of NP-Completeness. W. H. Freeman.

import pulp
import matplotlib.pyplot as plt

# Electoral votes for all 50 states and Washington D.C.
electoral_votes = [
    3, 11, 6, 9, 55, 9, 7, 3, 29, 16, 4, 4, 11, 6, 6, 8, 4, 6, 6, 10,
    11, 6, 10, 16, 10, 3, 4, 4, 3, 5, 15, 11, 3, 5, 18, 7, 7, 20, 9, 6,
    7, 3, 12, 8, 11, 3, 10, 14, 3, 5, 13  # Includes Washington D.C. (3 votes)
]

# Number of states
n = len(electoral_votes)

# Define the problem
problem = pulp.LpProblem("Maximize_Minimum_Subset_Sum", pulp.LpMaximize)

# Define variables
x = [pulp.LpVariable(f"x_{i}", cat="Binary") for i in range(n)]
t = pulp.LpVariable("t", lowBound=0, cat="Continuous")

# Objective function
problem += t

# Constraints
problem += pulp.lpSum([x[i] * electoral_votes[i] for i in range(n)]) >= t, "Subset 1 Minimum Sum"
problem += pulp.lpSum([(1 - x[i]) * electoral_votes[i] for i in range(n)]) >= t, "Subset 2 Minimum Sum"

# Solve the problem
problem.solve()

# Extract results
subset1 = [electoral_votes[i] for i in range(n) if x[i].varValue == 1]
subset2 = [electoral_votes[i] for i in range(n) if x[i].varValue == 0]
subset1_sum = sum(subset1)
subset2_sum = sum(subset2)

# Plotting the results
labels = ["Subset 1", "Subset 2"]
sizes = [subset1_sum, subset2_sum]
colors = ["skyblue", "salmon"]

plt.figure(figsize=(8, 6))
plt.pie(sizes, labels=labels, autopct='%1.1f%%', startangle=140, colors=colors)
plt.title("Closest Partition of US Electoral Votes (Integer Programming Solution)")
plt.show()

print("Subset 1:", subset1, "Sum:", subset1_sum)
print("Subset 2:", subset2, "Sum:", subset2_sum)
print("Difference:", abs(subset1_sum - subset2_sum))
print("Maximum minimum subset sum (t):", t.varValue)

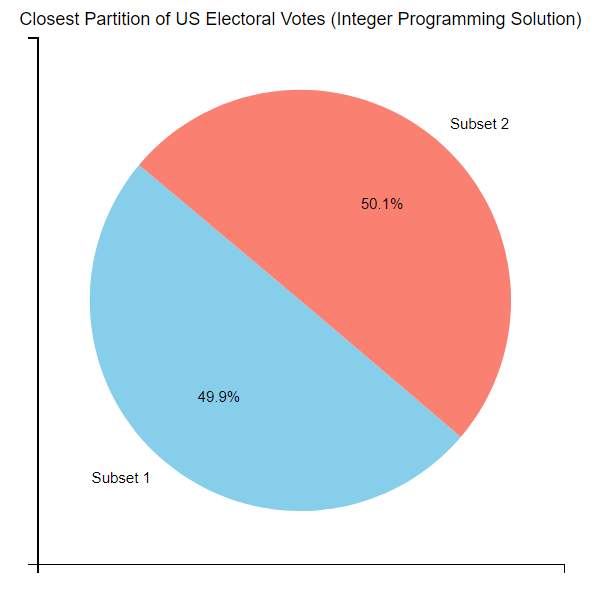
The graphic above shows the closest possible outcome in the U.S. Electoral College vote. Of course, blue and red can be used interchangeably. The conclusion is that there will always be a winner if the Electoral College delegates from each state vote unanimously for the candidate who won in their state.

The Partition Problem and the Possibility of an U.S. Electoral Stalemate

Share this:

Leave a comment Cancel reply