Interval Filters for Pre-Selection in Model-Assisted Constrained Pareto Optimization

Michael Emmerich, JYU, Finland, 28.1.2026

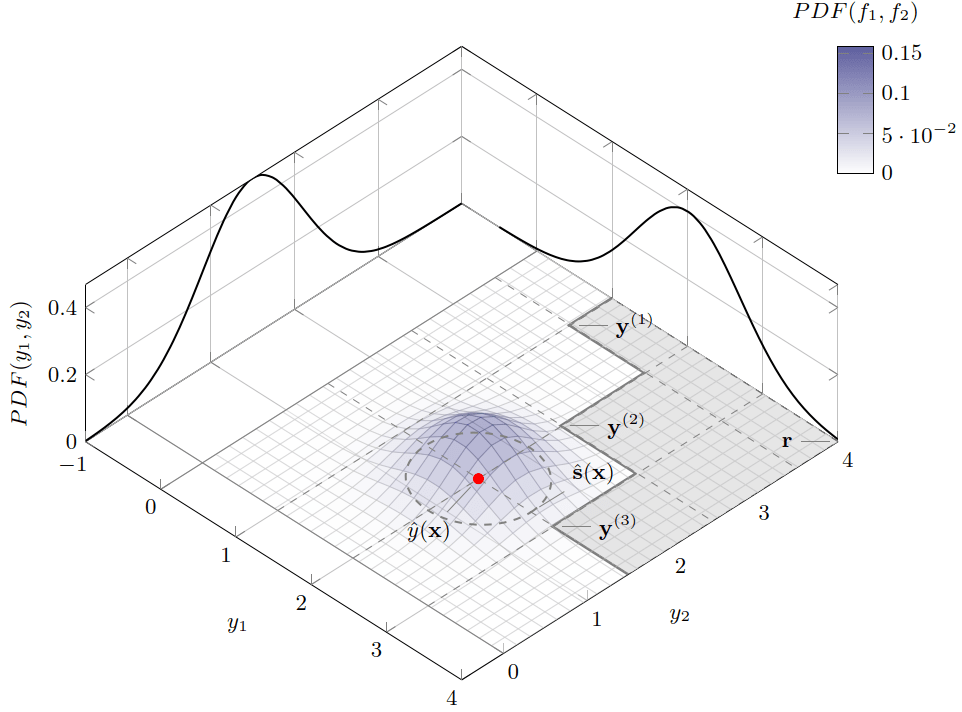
When objective and constraint evaluations are expensive (CFD/FEM, digital-twin simulations, etc.), we often rely on Gaussian process regression (Kriging) as a surrogate. A GP does not only predict a mean vector, it also delivers uncertainty. Interpreted component-wise, this uncertainty naturally forms an axis-aligned confidence box in $\mathbb{R}^m$ for $m$ objectives (and similarly for constraints). These boxes enable interval filters: crisp, dominance-based rules that can label candidates as certainly reject, possibly reject, or “keep for consideration,” before spending a single true evaluation.

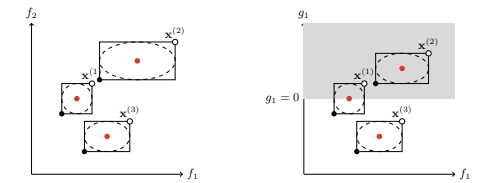
The core ideas go back to my 2005 PhD thesis (Emmerich, 2005) and were worked out for surrogate-assisted multiobjective selection and constraint handling in early 2004-era papers (see references at the end). A compact discussion of the interval-filter logic is also included in the attached book chapter (Section “Interval Filters,” with the illustrative figure of boxes in objective space and constraint space).

From GP/Kriging prediction to a “confidence box”

Assume minimization of $m$ objectives. For a candidate decision vector $\mathbf{x}$ , a GP provides a predictive mean $\hat{\mathbf{y}}(\mathbf{x})$ and predictive standard deviations $\hat{\mathbf{s}}(\mathbf{x})$ (component-wise, or from a diagonal approximation). Pick a width parameter $\omega > 0$ (e.g., tied to a desired coverage under a Gaussian assumption). Define lower/upper bounds per objective:

$\text{lb}_\omega(\mathbf{x})_i = \hat{y}_i(\mathbf{x}) - \omega \hat{s}_i(\mathbf{x})$ and $\text{ub}_\omega(\mathbf{x})_i = \hat{y}_i(\mathbf{x}) + \omega \hat{s}_i(\mathbf{x})$ .

Geometrically, the candidate is associated with the axis-aligned box $[\text{lb}_\omega(\mathbf{x}),\,\text{ub}_\omega(\mathbf{x})] \subset \mathbb{R}^m$ . In selection, this turns uncertain vectors into comparable objects: boxes.

Pareto dominance, now “lifted” to boxes

Recall (minimization): $\mathbf{a}$ dominates $\mathbf{b}$ if $a_i \le b_i$ for all $i$ and strict inequality holds for at least one component.

With boxes, we ask: can dominance be concluded for sure, or is it only possible depending on how the true values realize inside the boxes?

Certainly reject (certain dominance)

Let $\mathbf{x}$ be a candidate with bounds $(\text{lb}(\mathbf{x}),\text{ub}(\mathbf{x}))$ , and let $\mathbf{a}$ be another solution with bounds $(\text{lb}(\mathbf{a}),\text{ub}(\mathbf{a}))$ (or a fully evaluated point, in which case $\text{lb}(\mathbf{a})=\text{ub}(\mathbf{a})=\mathbf{f}(\mathbf{a})$ ).

A simple certain dominance test is: if $\text{ub}(\mathbf{a})$ dominates $\text{lb}(\mathbf{x})$ , then $\mathbf{x}$ is certainly dominated and can be labeled certainly reject.

Intuition: even if $\mathbf{x}$ realizes at its best-case corner ( $\text{lb}(\mathbf{x})$ ) and $\mathbf{a}$ realizes at its worst-case corner ( $\text{ub}(\mathbf{a})$ ), $\mathbf{a}$ still wins. So $\mathbf{x}$ cannot be non-dominated.

Possibly reject (possible dominance)

A weaker, “there exists a realization” test is: if $\text{lb}(\mathbf{a})$ dominates $\text{ub}(\mathbf{x})$ , then $\mathbf{x}$ is possibly dominated (in fact, dominated even under a very favorable realization for $\mathbf{x}$ ). More generally, if some realization inside the boxes allows $\mathbf{a}$ to dominate $\mathbf{x}$ , we call $\mathbf{x}$ possibly reject.

In practice, “possibly reject” is a tuning knob: using it aggressively increases precision (fewer poor evaluations) but risks losing recall (discarding candidates that could have been among the best). Interval filters make this trade-off explicit (often discussed as error types in pre-selection).

Constrained problems: certain vs possible feasibility

Now add inequality constraints $g_j(\mathbf{x}) \le 0$ for $j=1,\dots,k$ . Train surrogate(s) for constraints as well, producing bounds $\text{lb}^g_j(\mathbf{x})$ and $\text{ub}^g_j(\mathbf{x})$ in the same way as for objectives.

Certainly feasible: for all $j$ , $\text{ub}^g_j(\mathbf{x}) \le 0$ .
Certainly infeasible (hence certainly reject w.r.t. feasibility): for some $j$ , $\text{lb}^g_j(\mathbf{x}) > 0$ .
Possibly feasible: otherwise (the confidence interval crosses the boundary for at least one constraint).

A clean constrained-Pareto filter can then be phrased as: (i) reject everything that is certainly infeasible; (ii) among the remaining candidates, use box-dominance tests (above) but prioritize certainly feasible solutions over possibly feasible ones. This is exactly the kind of “interval picture” shown in the objective/constraint panels of the interval-filter figure in the attached chapter.

Figure: Illustration of confidence boxes in objective space for Pareto optimization, showing domination relationships between candidate solutions.

Where this fits in $\mu+\lambda$ selection

Consider we want to shortlist a list that comprises the best ${\mu}$ out of a list of ${\mu+\lambda}$ candidates. We can again apply possibilistic logic to maximize precision or to maximize recall based on the bounding boxes for the epistemic uncertainty. In a $(\mu+\lambda)$ evolution strategy (or any EA with parent+offspring elitist selection), we routinely have many offspring proposals $\lambda$ but can only afford to truly evaluate a small subset. Interval filters act as a dominance-based pre-screen:

Use GP/Kriging to assign a confidence box to each offspring (and optionally to unevaluated parents).
Apply certainly reject rules first (certain infeasibility and certain dominance).
From the remaining set, keep “possibly non-dominated / not certainly rejected” candidates for actual evaluation or for the next ranking stage (e.g., non-dominated sorting, hypervolume contribution, or exploration heuristics). The details for this step and are described in the attached PDF of a preprint.

The key point: GP/Kriging uncertainty is not just “error bars.” Treated as an $m$ -D confidence box, it gives logic-level statements (“cannot win”, “might win”) that are directly compatible with Pareto dominance and constraint satisfaction.

Emmerich___Early Ideas and Innovations (2006) preprint Download

M. Emmerich. Single- and Multi-Objective Evolutionary Design Optimization Assisted by Gaussian Random Field Metamodels. PhD thesis, University of Dortmund, 2005.
M. Emmerich. Python implementation of dynamic programming for minimum Riesz s-energy subset selection in ordered point sets. Zenodo, 10.5281/zenodo.14792491, 2025.
M. Emmerich, N. Beume, and B. Naujoks. An EMO algorithm using the hypervolume measure as selection criterion. In International Conference on Evolutionary Multi-Criterion Optimization, pages 62–76. Springer, 2005.
M. Emmerich, K. C. Giannakoglou, and B. Naujoks. Single- and multiobjective evolutionary optimization assisted by Gaussian random field metamodels. IEEE Transactions on Evolutionary Computation, 10(4):421–439, 2006.
M. Emmerich, A. Giotis, M. Özdemir, T. Bäck, and K. Giannakoglou. Metamodel-assisted evolution strategies. In International Conference on Parallel Problem Solving from Nature, pages 361–370. Springer, 2002.
M. Emmerich and B. Naujoks. Metamodel assisted multiobjective optimisation strategies and their application in airfoil design. In Adaptive Computing in Design and Manufacture VI, pages 249–260. Springer, 2004.
M. Emmerich and B. Naujoks. Metamodel-assisted multiobjective optimization with implicit constraints and its application in airfoil design. In International Conference & Advanced Course ERCOFTAC, Athens, Greece, 2004.
Limbourg, P., & Aponte, D. E. S. (2005, September). An optimization algorithm for imprecise multi-objective problem functions. In 2005 IEEE Congress on evolutionary computation (Vol. 1, pp. 459-466). IEEE.
M. T. M. Emmerich. Early ideas and innovations in Bayesian and model-assisted multiobjective optimization. In Challenges in Design Methods, Numerical Tools and Technologies for Sustainable Aviation, Transport and Industry, pp. 93–116, First Online: 28 January 2026. (Computational Methods in Applied Sciences, vol. 17). (Featured Article)https://doi.org/10.1007/978-3-031-98675-8_8