In diesem Beitrag versuche ich, auf einfache Weise darzustellen, wie mithilfe der Wahrscheinlichkeitsrechnung in einem Experiment festgestellt werden kann, ob ein System verborgene Variablen besitzt. Diese Methode ist von herausragender Bedeutung, da sie den statistischen Nachweis erbringt, dass Quantenkommunikation quasi instantan – also schneller als Lichtgeschwindigkeit – ablaufen kann. Gleichzeitig werden zentrale Prinzipien der Quantenmechanik erläutert, die für das Verständnis der Thematik unerlässlich sind.
Der Beitrag ist inspiriert von dem für Einsteiger sehr empfehlenswerten Buch Quantencomputing kompakt (Vol. 1) von Bettina Just (2023), erschienen bei Springer, Berlin.
Das Einstein-Podolsky-Rosen (EPR) Paradoxon
Im Jahr 1935 veröffentlichten Albert Einstein, Boris Podolsky und Nathan Rosen ein Paper, das die Vollständigkeit der Quantenmechanik infrage stellte. Sie argumentierten, dass, wenn die Quantenmechanik korrekt sei, es “spukhafte Fernwirkungen” geben müsse, bei denen sich zwei verschränkte Lichtteilchen (Photonen) über beliebige Entfernungen hinweg augenblicklich beeinflussen könnten. Diese Vorstellung widersprach dem Prinzip der Lokalität, wonach Informationen sich höchstens mit Lichtgeschwindigkeit ausbreiten können, oder, es gibt verborgene Variablen wie Einstein es hypothetisch annahm.
John Bell formulierte 1964 eine Ungleichung, die zeigte, dass jede Theorie mit lokalen verborgenen Variablen im Widerspruch zu den Vorhersagen der Quantenmechanik steht. Experimente, insbesondere von Alain Aspect in den 1980er Jahren, bestätigten, dass sich die Natur nicht durch lokale verborgene Variablen erklären lässt.
Bettina Just beschreibt in ihrem Buch dazu drei Experimente, und vermag es dadurch verständlich zu erklären was es mit der “spukhaften Wechselwirkung” genau auf sich hat, und warum Bell, mit dem dritten Experiment, die Hypothese von Einstein der verborgenen Variablen widerlegen konnte. Im folgenden ein Versuch einer Kurzfassung:
Klassisches Experiment mit nur einem Photon
Étienne‑Louis Malus war ein französischer Physiker, Ingenieur und Offizier, der vor allem durch seine Arbeiten zur Polarisation des Lichts bekannt wurde. Malus entdeckte 1809 das nach ihm benannte Malus’sche Gesetz. In seiner Veröffentlichung stellte er fest, dass die Intensität des linear polarisierten Lichts, das durch einen Polarisationsfilter (Polarisator) hindurchtritt, der Winkeldifferenz α zwischen dem Polarisationswinkel des einfallenden Lichts und der Durchlassachse des Polarisators nach der y = x cos²(α) Beziehung abnimmt. Die Intensität des Lichts beträgt x bevor das Licht den Filter passiert und y danach.
Das erste Experiment dient der Veranschaulichung von Malus’schen Gesetzes Experiment, allerdings wird hier wiederholt genau ein Photon von einer Photonenquelle ausgesendet. Das Photon trifft auf einen Polarisationsfilter. Sei α die Winkeldifferenz zwischen Polarisationsfilter und der Polarisierung des Photons. Dann wird laut das Photon mit der Wahrscheinlichkeit cos²(α) durchgelassen.
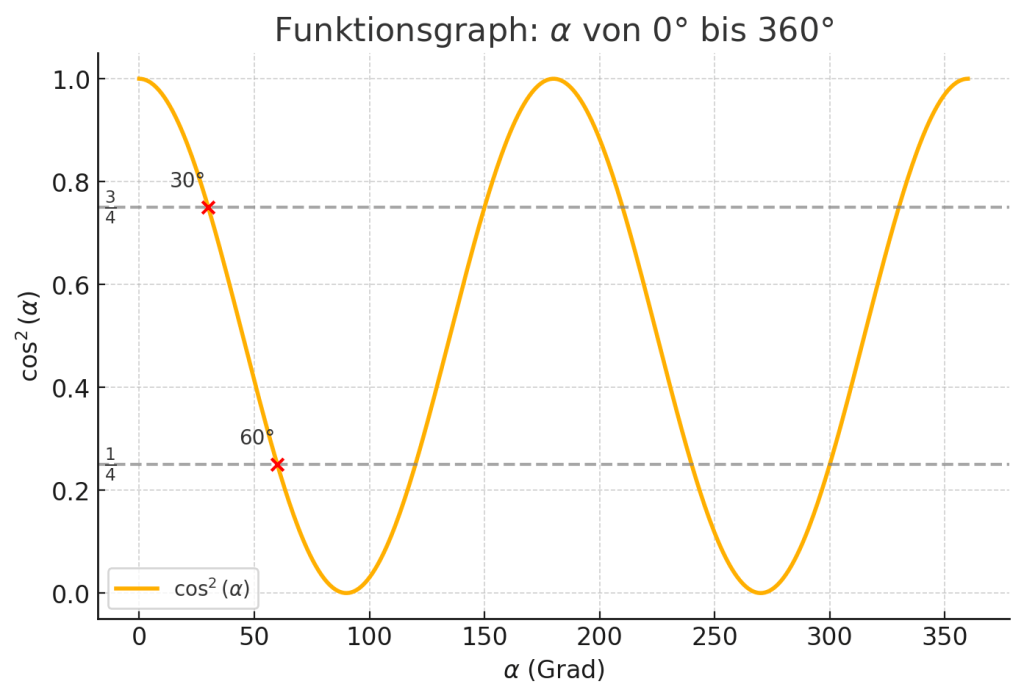
Zum Beispiel: Wenn die Winkeldifferenz 90° beträgt, wird das Photon sicher nicht durchgelassen, da cos²(90°) = 0. Andererseits passiert das Photon den Filter mit Wahrscheinlichkeit 1, wenn die Winkeldifferenz 0° oder 180° beträgt, da cos²(0°) = cos²(180°) = 1.
Für viele andere Winkeldifferenzen liegen die Werte zwischen 0 und 1,
beispielsweise: cos²(30°) = 3/4 und cos²(60°) = 1/4. Der Funktionsgraph unten illustriert das Verhalten der quadrierten Kosinus-Funktion.
EPR Experiment mit zwei verschränkten Photonen
Das folgende Experiment entspricht dem Experiment aus dem berühmten Artikel von Einstein, Podolsky und Rosen (1935). Alice und Bob befinden sich an verschiedenen Orten und wenden beide einen Polarisationsfilter mit derselben Ausrichtung sowie einen Detektor an, der genau gleichzeitig misst, ob das Photon passiert oder nicht.
Ein Photon wird von der Photonenquelle ausgesendet und in zwei miteinander verschränkte Photonen mit gleichem Polarisierungswinkel gespalten.
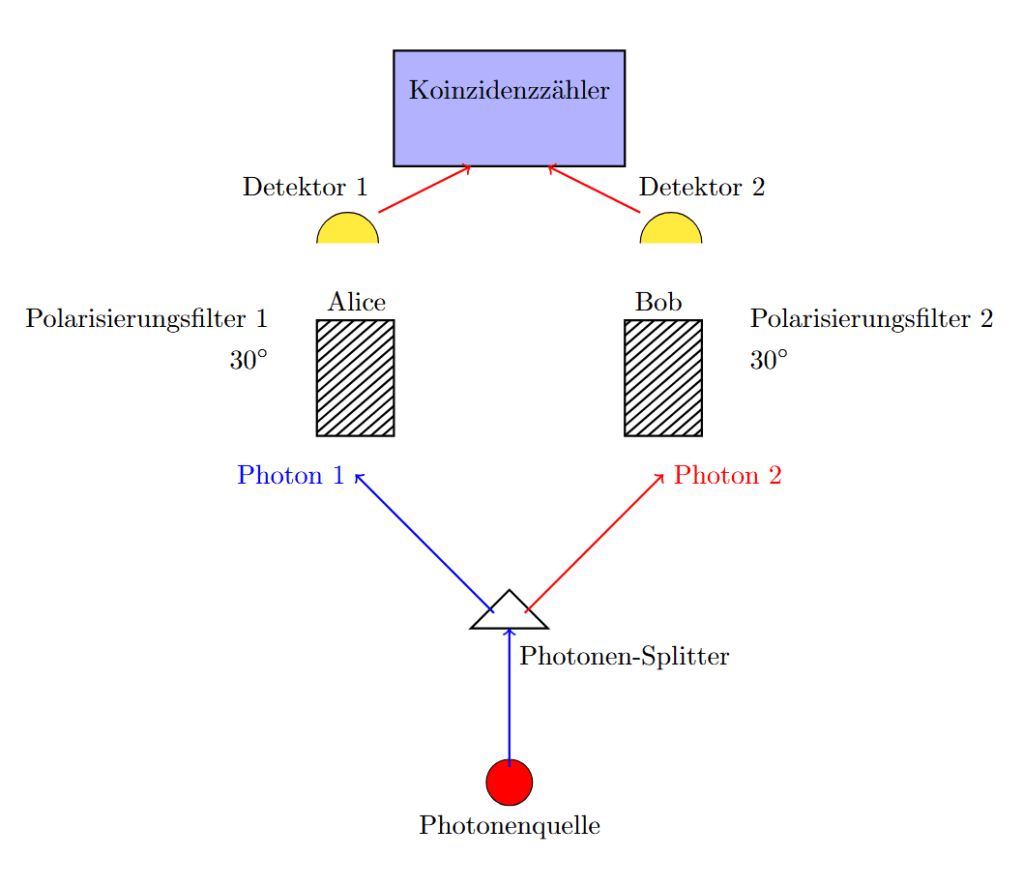
Das Ergebnis ist erstaunlich: Alice und Bob messen immer dasselbe Ergebnis (das Photon passiert oder passiert nicht), unabhängig vom Polarisationswinkel des Photons – als ob sich die Photonen „absprechen“ würden.
Die Wahrscheinlichkeiten entsprechen genau denen aus dem ersten Experiment: Alice misst nach der quadrierten Kosinusfunktion, und es scheint, als würde Bob überlichtschnell eine Botschaft erhalten und exakt dasselbe Ergebnis produzieren. Aber dann müssten sie sich schneller als das Licht „absprechen“, da die Photonen gleichzeitig auf die Polarisationsfilter treffen.
Alternativ müsste bereits im Voraus festgelegt sein, wie sich die Photonen
in verschiedenen Situationen (Winkel der Polarisationsfilter) „entscheiden“ würden.
Letzteres vermutete Albert Einstein und postulierte, dass es eine verborgene Variable geben müsse – eine Art Tabelle (oder Funktion), die die quadrierte Kosinusfunktion respektiert und für jeden Winkel eine Entscheidung vorgibt. Vielleicht entsteht diese Tabelle genau in dem Moment, in dem das ursprüngliche Photon gespalten wird, und wird beiden Photonen mitgegeben damit sie sich in jeder Situation gleich entscheiden. Die Hypothese von Einstein sollte sich als falsch erweisen, wie das im Folgenden erklärte raffinierte Experiment von Bell zeigte:
Bells Experiment mit zwei verschränkten Photonen
Zwei Hypothesen sollen gegeneinander getestet werden:
Hypothese 1: Es gibt verborgene Variablen (Einstein hatte dies vermutet). D.h. die Photonen haben sich schon vorher (bevor sie räumlich getrennt wurden) “abgesprochen” wie sie sich bei bestimmten Winkeln verhalten. Diese Absprache wird in verborgenen Variablen als Tabelle oder Funktion kodiert, je eine Variable (den Filter passieren=0, den Filter nicht passieren =1) pro Winkel.
Hypothese 2: Sie entscheiden sich erst beim Aufprall auf den Polarisationsfilter und stimmen sich instantan (quasi mit “Quanten-Teleportation”) aus, wie sie sich verhalten. Im Fall dass die Polarisationsfilter gleich sind verhalten sie sich gleich. Im Fall dass die Polarisierungsfilter um einen Winkel β verschieden sind entspricht die Wahrscheinlichkeit ob sie sich für das gleiche Ergebnis entscheiden der Winkeldifferenz (der Polarfilter), oder genauer cos(β)².
Das hieße – und dieses Beispiel ist wichtig für das Verständnis von Bells Experiment – dass im Fall von Hypothese 2 beispielsweise bei einer Winkeldifferenz von β = 0 stets das gleiche Ergebnis erzielt wird. Bei einer Winkeldifferenz von β = 30 tritt das gleiche Ergebnis mit einer Wahrscheinlichkeit von 3/4 auf, während bei β = 60 dieses Ergebnis nur mit einer Wahrscheinlichkeit von 1/4 erzielt wird (bzw. mit einer Wahrscheinlichkeit von 3/4 ein unterschiedliches Ergebnis).
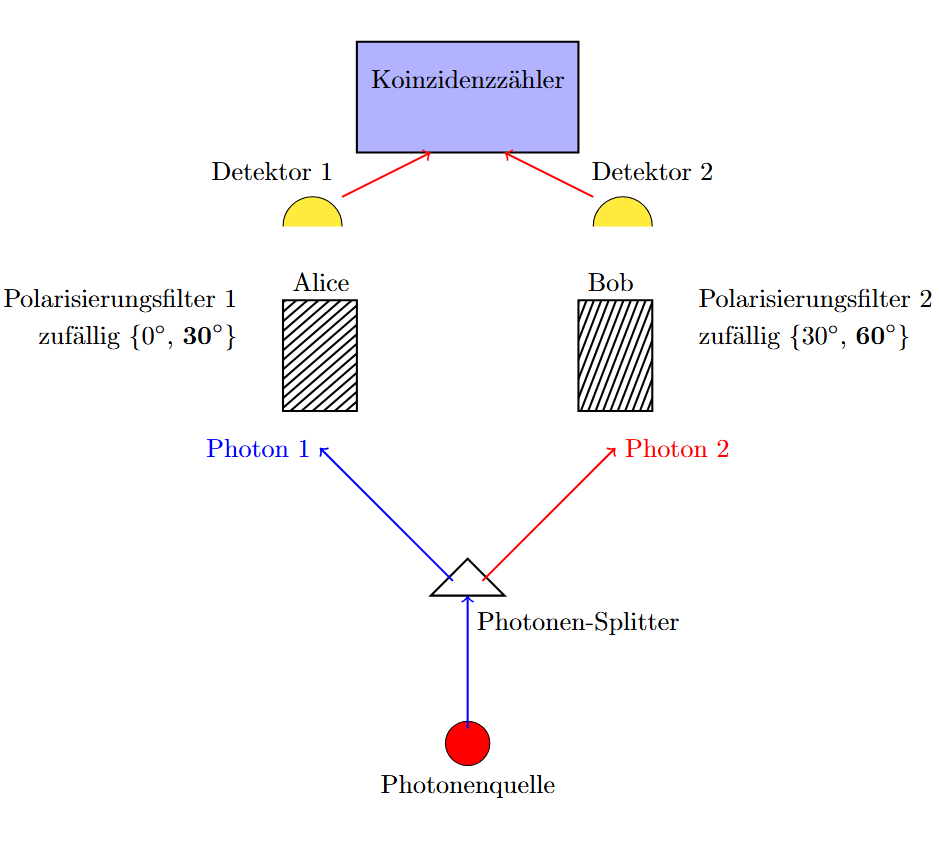
In Bells Experiment untersuchen Alice und Bob die Polarisation verschränkter Photonen. Ein Photon verlässt die Photonenquelle mit einer zufälligen Polarisation. Ein Photonensplitter macht aus dem einen Photon zwei miteinander verschränkte Photonen mit kleinerer Energie. Diese werden durch Spiegel in jeweils unterschiedliche Richtungen gelenkt. Photon 1 nach Alice und Photon 2 nach Bob der, und das ist wichtig, sehr weit von Alice entfernt ist. Bell wendet in seinem Vorschlag um Hypothese 1 versus Hypothese 2 zu entscheiden genau drei Filtertypen an.
- Alice’s Filter: Alice hat zwei mögliche Filterausrichtungen: einen bei 0° und einen bei 30°.
- Bob’s Filter: Bob hat ebenfalls zwei mögliche Filterausrichtungen: einen bei 30° und einen bei 60°.
In jedem Durchlauf des Experiments wählen Alice und Bob zufällig eine der beiden verfügbaren Einstellungen, und, dass ist wichtig, sie wählen die Ausrichtung nachdem die Photonen gesplittet wurden. Diese Anordnung führt zu unterschiedlichen Winkeldifferenzen zwischen ihren Filtern:
- Wenn beide 30° wählen: Der relative Winkel beträgt 0°
- Wenn die Winkeldifferenz 30° beträgt: Dies tritt beispielsweise ein, wenn Alice 0° wählt, während Bob 30° wählt, oder wenn Alice 30° wählt, während Bob 60° wählt.
- Wenn die Winkeldifferenz 60° beträgt: Bei der Kombination, in der Alice 0° wählt und Bob 60° wählt, beträgt der relative Winkel 60°. (In vielen Darstellungen liegt der Fokus auf den Unterschieden von 0° und 30°, um die Verletzung der lokal-realistischen Vorhersagen zu verdeutlichen; Details zu 60° können separat analysiert werden.)
Dabei ist das Messergebnis 0 “Absorbiert” und 1 “Photon passiert den Filter” in diesen Fällen proportional zu cos(𝛼)² wobei 𝛼 wieder die Winkeldifferenz zwischen dem Polarisationsfilter und der Polarisierung des Photons ist.
Hier ist das Messergebnis, welches im Folgenden alternativ mit Hypothese 1 oder Hypothese 2 zu erläutern ist:
Wenn beide 30° wählen: Hier messen beide das gleiche Ergebnis, entsprechend dem zweiten Experiment und dieses könnte man sowohl durch Hypothese 1 und Hypothese 2 erklären.
Wenn die Winkeldifferenz 30° beträgt: Hier messen Alice und Bob mit der Wahrscheinlichkeit 3/4 das gleiche. Dieses Ergebnis lässt sich, wie wir im Folgenden erläutern, mit Hypothese 2 erklären und steht im Widerspruch zu Hypothese 1.
Wenn der relative Winkel 60° beträgt: Hier messen Alice und Bob mit der Wahrscheinlichkeit 3/4 unterschiedliche Ergebnisse.
Versuch einer Erklärung mit Hypothese 1: Erwartung unter Annahme verborgener Variablen
Wir definieren drei zufällige verborgene Variablen x1, x2, x3, die die vor dem Split ‘abgesprochenen’ Messungen der Dektektoren im Fall dass das Photon auf einen Polarisationsfilter 0°, 30° und 60° trifft festlegen. Und zeigen dann dass egal wie wir die verborgenen Variablen festlegen die theoretischen Wahrscheinlichkeiten mit den real gemessenen Wahrscheinlichkeiten im Widerspruch stehen.
Die relevanten Messwinkelkombinationen der Polarisationsfilter sind:
- 0° (A0) und 30° (B30)
- 30° (A30) und 60° (B60)
- 0° (A0) und 60° (B60)
Wenn verborgene Variablen existieren und die Messergebnisse vollständig bestimmen, dann ist die Wahrscheinlichkeit, dass Alice und Bob mit „Ja“ antworten, höchstens 2/3. Dies geht aus der im folgenden dargestellten Tabelle hervor.
Die Tabelle umfasst alle möglichen Annahmen über im Vorraus bestimmte verborgene Variablen. Auf der rechten Seite sind die Ereignisse aufgetragen.
| Wert der Variable | Wert der Variable | Wert der Variable | Ereignis (P=1/3) | Ereignis (P=1/3) | Ereignis (P=1/3) |
|---|---|---|---|---|---|
| x1: Mess-ergebnis bei 0° | x2: Mess-ergebnis bei 30° | x3: Mess-ergebnis bei 60° | Alice wählt 0° und Bob 30° Ergebnis gleich | Alice wählt 30° und Bob 60° Ergebnis gleich | Alice wählt 0° und Bob 60° Ergebnis ungleich |
| 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 |
Interpretation der Tabelle: Egal, wie wir die verborgenen Variablen wählen, die Wahrscheinlichkeit, dass eines der drei Ereignisse zutrifft, ist stets kleiner oder gleich 2/3, und das ist wichtig: das Ergebnis die Wahrscheinlichkeit ist immer deutlich kleiner als die statistisch gemessene Wahrscheinlichkeit 3/4.
Versuch einer Erklärung mit Hypothese 2
Wenn wir allerdings annehmen, dass die Messergebnisse erst im Moment der Messung festgelegt werden, erscheint es plausibel, dass das jeweils gewählte Ereignis mit einer Wahrscheinlichkeit von 3/4 eintritt.
Gemäß den Gesetzen der Quantenmechanik gilt: cos²(30°) = 3/4 und cos²(60°) = 1/4 (also 1 – 3/4). Wenn also Alices Photon sich nach der Messung quasi instantan mit Bobs Photon Informationen austauschen könnte – sodass es sich gemäß eines der beiden Filter zunächst polarisiert und anschließend auf den jeweils anderen Filter trifft – wäre das tatsächlich gemessene Ergebnis mit einer Wahrscheinlichkeit von 3/4 erklärbar.
Interpretation: “Spukhafte Fernwirkung”
Da die experimentellen Wahrscheinlichkeiten nicht mit lokalen verborgenen Variablen erklärt werden können, und die Hypothese, dass die Messergebnisse erst zum Zeitpunkt der Messung “entschieden” werden erklärt die Messungen besser. Dies könnte bedeuten, dass sich die Photonen “instantan” absprechen müssen, was das Konzept einer lokalen Realität infrage stellt. Die beiden miteinander verschränkten Photonen kennen ihr Ergebnis in verschiedenen Situationen also nicht im Voraus, sondern werden erst bei der Messung festgelegt – unabhängig von der Entfernung zwischen ihnen. Dies widerspricht dem klassischen Weltbild, ist aber eine zentrale Eigenschaft der Quantenmechanik.
Eine bisher unbeantwortete Frage ist, ob Alice und Bob überlichtschnelle Kommunikation realisieren können. Nach unserem aktuellen Wissensstand ist dies jedoch nicht möglich. Die sogenannte Quantenteleportation stellt ein Verfahren dar, bei dem mithilfe verschränkter Quanten Informationen übertragen werden. Das Protokoll wird in Kapitel 11 von Bettina Justs Buch ausführlich erläutert und kann nur mit Hilfe von Quanten-Gates vollständig verstanden werden. Der limitierende Faktor besteht allerdings darin, dass nach der Messung ein Austausch von Informationen über klassische Kommunikationskanäle notwendig ist, um festzustellen, ob die Messergebnisse von Alice und Bob übereinstimmten.
Literatur
- Einstein, A., Podolsky, B., & Rosen, N. (1935). “Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?” Physical Review, 47(10), 777–780. DOI: 10.1103/PhysRev.47.777
- Bell, J. S. (1964). “On the Einstein Podolsky Rosen Paradox.” Physics Physique Физика, 1(3), 195–200. DOI: 10.1103/PhysicsPhysiqueFizika.1.195
- Bell, J. S. (1966). On the problem of hidden variables in quantum mechanics. Reviews of Modern physics, 38(3), 447.
- Aspect, Alain, Philippe Grangier, and Gérard Roger. “Experimental tests of realistic local theories via Bell’s theorem.” Physical review letters 47.7 (1981): 460.
- Just, Bettina (2023). Quantum computing compact (Vol. 1). Springer, Berlin, Germany
- Just, Bettina (2020). Quantencomputing kompakt: Spukhafte Fernwirkung und Teleportation endlich verständlich, Springer Vieweg