Uniformly Lighting the Christmas Tree: Riesz s-Energy in Action
Uniformly Lighting the Christmas Trees: Riesz -Energy in Action
Michael Emmerich, December 25th, 2024
Did you ever have the problem of how to distribute candles uniformly across your Christmas Tree? Well, here is a solution from the mathematical sciences! Using the concept of Riesz -Energy, we can optimize the placement of stars or candles on a tree-like structure to achieve a uniform distribution. This post describes the process of creating a “Riesz -Energy Christmas Tree,” where the candles are visualized as points distributed evenly over the surface of a cone by minimizing the -energy function.
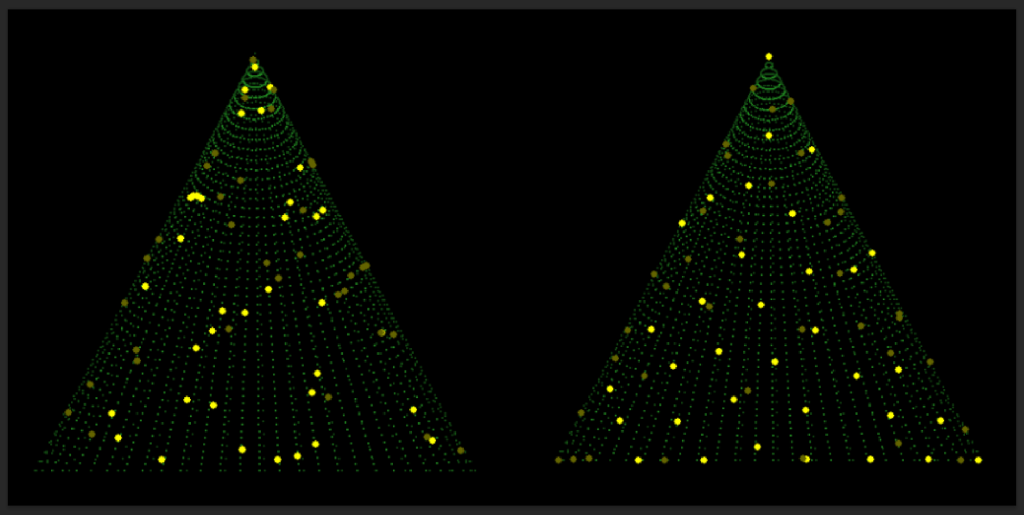
In this post, we explore the intriguing visualization of Riesz -energy optimization over a spherical cone. This process involves distributing a set of points (or candles, as visualized in our Python implementation) uniformly over the surface of a cone by minimizing the -energy function. The visualization is created using pygame (see link at the end of essay), and the optimization employs simulated annealing to minimize the Riesz s-Energy of the configuration of points. For theoretical insights, this blog also discusses the application of simulated annealing to Riesz -energy problems and their connection to uniform distributions on rectifiable manifolds.
Riesz -Energy is named after the Hungarian mathematician Marcel Riesz (1886–1969). Originally developed in the context of electrophysics, it was used to analyze the distribution of electrons. The Coulomb energy is a special case of Riesz -Energy when . Recently, Riesz -Energy has also seen recent applications as a diversity indicator to distribute point sets evenly across approximations of trade-off surfaces (Pareto fronts) in multi-objective optimization (Falcon-Cardona et al. 2024), triggering a renewed interest in pairwise potentials in other domains than physics.
Theoretical Background
The Riesz -energy for a set of points on a manifold is defined as:
where denotes the Euclidean distance between points and , and
is a parameter that controls the strength of repulsion between points.
As shown in (Hardin et al., 2005), minimizing for -energy problems tends to distribute points uniformly on rectifiable manifolds as grows. This finding is sometimes referred to as the “poppz seed bagel theorem”. Here, we focus on the surface of a spherical cone, a manifold defined by its height and base radius.
Simulated Annealing for -Energy Optimization
Simulated annealing is an iterative optimization algorithm inspired by the cooling of materials. At each step, the algorithm perturbs the current configuration of points and evaluates the change in energy. The perturbation is accepted probabilistically, based on the temperature , which decreases gradually:
For this visualization, we initialize random points on the cone surface and optimize their positions over 50,000 iterations. The cooling schedule starts with and uses an exponential cooling rate of .
Python Implementation
The interactive Python program uses pygame for real-time visualization of the optimization process. Each point on the cone is parameterized by (angle) and (height). This parametrization allows easy visibility checks by means of checking whether the angle is in a prescribed interval. The program calculates the -energy of (perturbed) point configurations and dynamically updates the positions of the points, projecting them into 2D for rendering.
The visualization reveals how the points (candles) converge to a near-uniform distribution on the spherical cone surface as the optimization progresses. The simulated annealing algorithm efficiently explores the solution space, minimizing the -energy function.
References
D.P. Hardin and E.B. Saff, Minimal Riesz energy point configurations for rectifiable -dimensional manifolds, Advances in Mathematics, 2005.
J.G. Falcón-Cardona, L. Uribe, and P. Rosas, Riesz -Energy as a Diversity Indicator in Evolutionary Multi-Objective Optimization, IEEE Transactions on Evolutionary Computation, 2024.
Michael Emmerich 